This article is part of the Multiple Imputation in Stata series. For a list of topics covered by this series, see the Introduction.
This article contains examples that illustrate some of the issues involved in using multiple imputation. Articles in the Multiple Imputation in Stata series refer to these examples, and more discussion of the principles involved can be found in those articles. However, it is possible to read this article independently, or to just read about the particular example that interests you (see the list of examples below).
These examples are not intended to test the validity of the techniques used or rigorously compare their effectiveness. However, they should give you some intuition about how they work and their strengths and weaknesses. Some of the simulation parameters (and occasionally the seed for the random number generator) were chosen in order to highlight the issue at hand, but none of them are atypical of real-world situations. The data are generated randomly from standard distributions in such a way that the "right" answers are known and you can see how closely different techniques approach those answers.
A Stata do file is provided for each example, along with commentary and selected output (in this web page). The do file also generates the data set used, with a set seed for reproducibility. Our suggestion is that you open the do file in Stata's do file editor or your favorite text editor and read it in parallel with the discussion in the article. Please note that the example do files are not intended to demonstrate the entire process of multiple imputation—they don't always check the fit or convergence of the imputation models, for example, which are very important things to do in real world use of multiple imputation.
Each example concludes with a "Lessons Learned" section, but we'd like to highlight one overall lesson: Multiple imputation can be a useful tool, but there are many ways to get it wrong and invalidate your results. Be very careful, and don't expect it to be quick and easy.
The examples are:
- Power
- MCAR vs. MAR vs. MNAR
- Imputing the Dependent Variable
- Non-Normal Data
- Transformations
- Non-Linearity
- Interactions
Power
The most common motivation for using multiple imputation is to try to increase the power of statistical tests by increasing the number of observations used (i.e. by not losing observations due to missing values). In our experience it rarely makes a large difference in practice. This example uses ideal circumstances to illustrate what extremely successful multiple imputation would look like.
Data
Observations: 1,000
Variables:
- x1-x10 drawn from standard normal distribution (independently)
- y is the sum of all x's, plus a normal error term
Missingness: Each value of the x variables has a 10% chance of being missing (MCAR).
Right Answers: Regressing y on all the x's, each x should have a coefficient of 1.
Procedure
Begin with complete cases analysis:
Source | SS df MS Number of obs = 369
-------------+------------------------------ F( 10, 358) = 6.71
Model | 3882.86207 10 388.286207 Prob > F = 0.0000
Residual | 20722.7734 358 57.884842 R-squared = 0.1578
-------------+------------------------------ Adj R-squared = 0.1343
Total | 24605.6355 368 66.86314 Root MSE = 7.6082
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .733993 .4216582 1.74 0.083 -.0952453 1.563231
x2 | 1.664231 .3867292 4.30 0.000 .903684 2.424777
x3 | 1.51406 .3907875 3.87 0.000 .7455327 2.282588
x4 | .2801067 .395164 0.71 0.479 -.4970278 1.057241
x5 | .8524305 .4076557 2.09 0.037 .0507297 1.654131
x6 | .7704437 .413519 1.86 0.063 -.042788 1.583675
x7 | .6512155 .3938107 1.65 0.099 -.1232575 1.425689
x8 | .9173208 .3969585 2.31 0.021 .1366572 1.697984
x9 | .8736406 .4115488 2.12 0.034 .0642835 1.682998
x10 | .9222064 .4123417 2.24 0.026 .11129 1.733123
_cons | -.1999121 .3975523 -0.50 0.615 -.9817434 .5819192
------------------------------------------------------------------------------
Note that although each x value has just a 10% chance of being missing, because we have ten x variables per observation almost 2/3 of the observations are missing at least one value and must be dropped. As a result, the standard errors are quite large, and the coefficients on four of the ten x's are not significantly different from zero.
After multiple imputation, the same regression gives the following:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.1483
Largest FMI = 0.2356
Complete DF = 989
DF adjustment: Small sample DF: min = 142.63
avg = 425.17
max = 928.47
Model F test: Equal FMI F( 10, 802.0) = 18.13
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .793598 .2679515 2.96 0.003 .2657743 1.321422
x2 | 1.133405 .2482047 4.57 0.000 .6460259 1.620785
x3 | 1.33182 .2521916 5.28 0.000 .8364684 1.827172
x4 | 1.159887 .2714759 4.27 0.000 .624309 1.695465
x5 | 1.181207 .2901044 4.07 0.000 .607747 1.754667
x6 | 1.305636 .2835268 4.60 0.000 .7466279 1.864645
x7 | .6258813 .2568191 2.44 0.015 .121268 1.130494
x8 | 1.143631 .253376 4.51 0.000 .6461328 1.64113
x9 | 1.112347 .2838261 3.92 0.000 .5520503 1.672644
x10 | 1.053309 .2612807 4.03 0.000 .5397648 1.566854
_cons | .0305628 .2499378 0.12 0.903 -.4599457 .5210712
------------------------------------------------------------------------------
The standard errors are much smaller than with complete cases analysis, and all of the coefficients are significantly different from zero. This illustrates the primary motivation for using multiple imputation.
Lessons Learned
This data set is ideal for multiple imputation because it has large numbers of observations with partial data. Complete cases analysis must discard all these observations. Multiple imputation can use the information they contain to improve the results.
Note that the imputation model could not do a very good job of predicting the missing values of the x's based on the observed data. The x's are completely independent of each other and thus have no predictive power. y has some but not much: if you regress each x on y and all the other x's (which is what the imputation model used does), the R-squared values are all less than 0.1 and most are less than 0.03. The success of multiple imputation does not depend on imputing the "right" values of the missing variables for individual observations, but rather on correctly modeling their distribution conditional on the observed data.
MCAR vs. MAR vs. MNAR
Whether your data are Missing Completely at Random (probability of being missing does not depend on either observed or unobserved data), Missing at Random (probability of being missing depends only on observed data), or Missing Not at Random (probability of being missing depends on unobserved data) is very important in deciding how to analyze it. This example shows how complete cases analysis and multiple imputation respond to different mechanisms for missingness.
Data
Observations: 1,000
Variables:
- x is drawn from standard normal distribution
- y is x plus a normal error term
Missingness:
- y is always observed
- First run: probability of x being missing is 10% for all observations (MCAR)
- Second run: probability of x being missing is proportional to y (MAR)
- Third run: probability of x being missing is proportional to x (MNAR)
Right Answers: Regressing y on x, x should have a coefficient of 1.
Procedure
We'll analyze this data set three times, once when it is MCAR, once when it is MAR, and once when it is MNAR.
MCAR
In the first run, the data set is MCAR and both complete cases analysis and multiple imputation give unbiased results.
Complete cases analysis:
Source | SS df MS Number of obs = 882
-------------+------------------------------ F( 1, 880) = 932.47
Model | 918.60551 1 918.60551 Prob > F = 0.0000
Residual | 866.913167 880 .985128598 R-squared = 0.5145
-------------+------------------------------ Adj R-squared = 0.5139
Total | 1785.51868 881 2.02669543 Root MSE = .99254
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9842461 .0322319 30.54 0.000 .9209858 1.047506
_cons | -.0481664 .0334249 -1.44 0.150 -.1137683 .0174354
------------------------------------------------------------------------------
Multiple imputation:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.1112
Largest FMI = 0.1583
Complete DF = 998
DF adjustment: Small sample DF: min = 262.51
avg = 541.98
max = 821.46
Model F test: Equal FMI F( 1, 821.5) = 1014.02
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9837383 .0308928 31.84 0.000 .9231003 1.044376
_cons | -.0377668 .0342445 -1.10 0.271 -.1051958 .0296621
------------------------------------------------------------------------------
MAR
Now, consider the case where the probability of x being missing is proportional to y (which is always observed), making the data MAR. With MAR data, complete cases analysis is biased:
Source | SS df MS Number of obs = 652
-------------+------------------------------ F( 1, 650) = 375.85
Model | 252.090968 1 252.090968 Prob > F = 0.0000
Residual | 435.966034 650 .670716976 R-squared = 0.3664
-------------+------------------------------ Adj R-squared = 0.3654
Total | 688.057002 651 1.0569232 Root MSE = .81897
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .6857927 .035374 19.39 0.000 .6163317 .7552538
_cons | -.558313 .0352209 -15.85 0.000 -.6274736 -.4891525
------------------------------------------------------------------------------
However, multiple imputation gives unbiased estimates:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.4234
Largest FMI = 0.3335
Complete DF = 998
DF adjustment: Small sample DF: min = 78.63
avg = 90.20
max = 101.78
Model F test: Equal FMI F( 1, 78.6) = 750.78
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9909115 .0361642 27.40 0.000 .9189232 1.0629
_cons | -.0544014 .0366092 -1.49 0.140 -.1270175 .0182146
------------------------------------------------------------------------------
MNAR
Finally consider the case where the probability of x being missing proportional to x. This makes the data missing not at random (MNAR), and with MNAR data both complete cases analysis and multiple imputation are biased.
Complete cases analysis:
Source | SS df MS Number of obs = 679
-------------+------------------------------ F( 1, 677) = 463.29
Model | 464.94386 1 464.94386 Prob > F = 0.0000
Residual | 679.422756 677 1.00357866 R-squared = 0.4063
-------------+------------------------------ Adj R-squared = 0.4054
Total | 1144.36662 678 1.68785636 Root MSE = 1.0018
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 1.093581 .0508074 21.52 0.000 .9938225 1.19334
_cons | .0420364 .0469578 0.90 0.371 -.050164 .1342368
------------------------------------------------------------------------------
Multiple imputation:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.3930
Largest FMI = 0.3425
Complete DF = 998
DF adjustment: Small sample DF: min = 74.96
avg = 144.00
max = 213.04
Model F test: Equal FMI F( 1, 75.0) = 561.03
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 1.223772 .0516665 23.69 0.000 1.120846 1.326698
_cons | .3816984 .0402614 9.48 0.000 .3023366 .4610602
------------------------------------------------------------------------------
Complete cases analysis actually does better with this particular data set, but that's not true in general.
Lessons Learned
Always investigate whether your data set is plausibly MCAR or MAR. (For example, run logits on indicators of missingness and see if anything predicts it—if it does the data set is MAR rather than MCAR.) If your data set is MAR, consider using multiple imputation rather than complete cases analysis.
MNAR, by definition, cannot be detected by looking at the observed data. You'll have to think carefully about how the data was collected and consider whether some values of the variables might make the data more or less likely to be observed. Unfortunately, the options for working with MNAR data are limited.
Imputing the Dependent Variable
Many researchers believe it is inappropriate to use imputed values of the dependent variable in the analysis model, especially if the variables used in the imputation model are the same as the variables used in the analysis model. The thinking is that the imputed values add no information since they were generated using the model that is being analyzed.
Unfortunately, this sometimes is misunderstood as meaning that the dependent variable should not be included in the imputation model. That would be a major mistake.
Complete code for this example
Data
Observations: 1,000
Variables:
- x1-x3 drawn from standard normal distribution (independently)
- y is the sum of all x's, plus a normal error term
Missingness: y and x1-x3 have a 20% probability of being missing (MCAR).
Right Answers: Regressing y on x1-x3, the coefficient on each should be 1.
Procedure
The following are the results of complete cases analysis:
Source | SS df MS Number of obs = 4079
-------------+------------------------------ F( 3, 4075) = 3944.41
Model | 12264.8582 3 4088.28608 Prob > F = 0.0000
Residual | 4223.63457 4075 1.03647474 R-squared = 0.7438
-------------+------------------------------ Adj R-squared = 0.7437
Total | 16488.4928 4078 4.04327926 Root MSE = 1.0181
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .9834974 .0160921 61.12 0.000 .9519481 1.015047
x2 | 1.000172 .0160265 62.41 0.000 .9687511 1.031593
x3 | 1.003089 .0159724 62.80 0.000 .9717744 1.034404
_cons | -.0003362 .0159445 -0.02 0.983 -.0315962 .0309238
------------------------------------------------------------------------------
If you leave y out of the imputation model, imputing only x1-x3, the coefficients on the x's in the final model are biased towards zero:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 7993
Average RVI = 0.4014
Largest FMI = 0.3666
Complete DF = 7989
DF adjustment: Small sample DF: min = 72.62
avg = 119.53
max = 161.84
Model F test: Equal FMI F( 3, 223.0) = 1761.75
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .7946113 .0185175 42.91 0.000 .7580219 .8312007
x2 | .7983325 .0199962 39.92 0.000 .7584766 .8381885
x3 | .8001109 .0193738 41.30 0.000 .7616436 .8385782
_cons | .0041643 .0183891 0.23 0.821 -.0321492 .0404778
------------------------------------------------------------------------------
Why is that? An easy way to see the problem is to look at correlations. First, the correlation between y and x1 in the unimputed data:
| y x1
-------------+------------------
y | 1.0000
x1 | 0.5032 1.0000
Now, the correlation between y and x1 for those observations where x1 is imputed (this is calculated for the first imputation, but the others are similar):
| y x1
-------------+------------------
y | 1.0000
x1 | -0.0073 1.0000
Because y is not included in the imputation model, the imputation model creates values of x1 (and x2 and x3) which are not correlated with y. This does not match the observed data. It also biases the results of the final model by adding observations in which y really is unrelated to x1, x2, and x3.
This problem goes away if y is included in the imputation model. Given the nature of chained equations, this means that values of y must be imputed. However, you're under no obligation to use those values in your analysis model. Simply create an indicator variable for "y is missing in the observed data," which can be done automatically with misstable sum, gen(miss_), and then add if !miss_y to the regression command. This restricts the regression to those observations where y is actually observed, so any imputed values of y are not used. Here are the results:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 7993
Average RVI = 0.6402
Largest FMI = 0.5076
Complete DF = 7989
DF adjustment: Small sample DF: min = 38.27
avg = 82.39
max = 182.83
Model F test: Equal FMI F( 3, 137.9) = 4691.72
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .9852388 .0150348 65.53 0.000 .9550372 1.01544
x2 | .9923264 .0158077 62.77 0.000 .9603327 1.02432
x3 | .9936324 .0129186 76.91 0.000 .9681437 1.019121
_cons | -.0015309 .0145755 -0.11 0.917 -.0306997 .0276378
------------------------------------------------------------------------------
On the other hand, using the imputed values of y turns out to make almost no difference in this case (see the complete code).
Lessons Learned
Always include the dependent variable in your imputation model. Whether you should use imputed values of the dependent variable in your analysis model is unclear, but always impute them.
Non-Normal Data
The obvious way to impute a continuous variable is regression (i.e. the regress command in mi impute chained). However, it applies a normal error term. What happens if a variable is not at all normally distributed?
Complete code for this example
Data
Observations: 10,000
Variables:
- g is a binary (1/0) variable with a 50% probability of being 1
- x is drawn from the standard normal distribution, then 5 is added if g is 1. Thus x is bimodal.
- y is x plus a normal error term
Missingness: Both y and x have a 10% probability of being missing (MCAR).
Right Answers: Regressing y on x, x should have a coefficient of 1.
Procedure
Given the way x was constructed, it has a bimodal distribution and is definitely not normal:
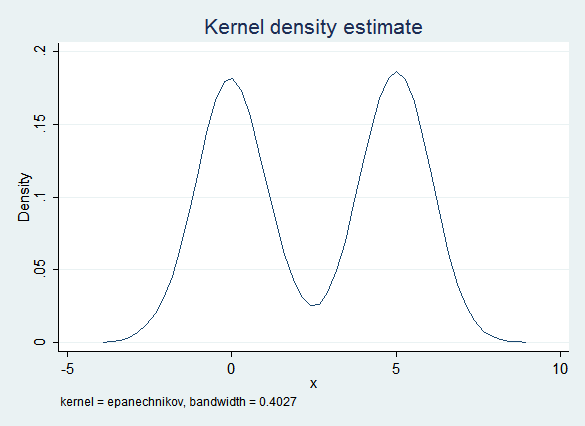
The obvious imputation model (regress x on y) captures some of this bimodality because of the influence of y. However, the error term is normal and does not take into account the non-normal distribution of the data. Thus this model is too likely to create imputed values that are near 2.5 (the "valley" between the two "peaks") and the distribution of the imputed data is "too normal":
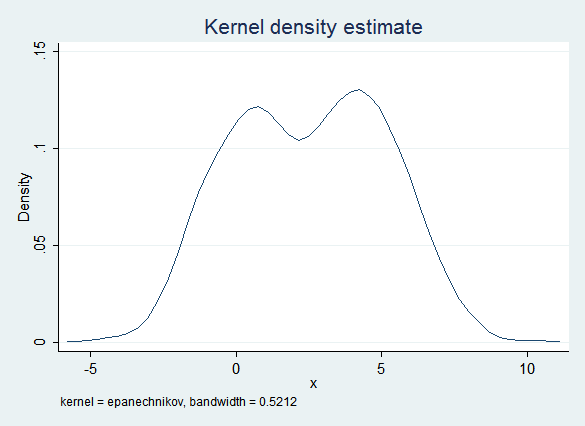
However, the regression results are quite good:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.2471
Largest FMI = 0.1977
Complete DF = 9998
DF adjustment: Small sample DF: min = 238.92
avg = 414.68
max = 590.43
Model F test: Equal FMI F( 1, 590.4) = 63916.86
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 1.001225 .0039603 252.82 0.000 .9934473 1.009003
_cons | -.0068119 .0152489 -0.45 0.655 -.0368514 .0232276
------------------------------------------------------------------------------
Replacing regression with Predictive Mean Matching gives a much better fit. PMM begins with regression, but it then finds the observed value of x that is the nearest match. Because there are fewer observed values in the "valley" PMM is less likely to find a match there, resulting in a distribution that is closer to the original:
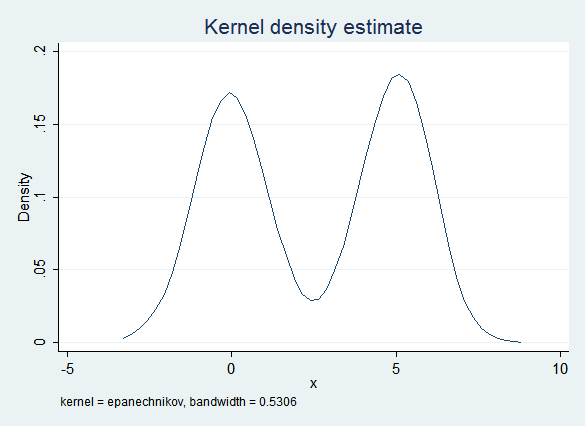
Regression results after imputing with PMM are also good:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.2885
Largest FMI = 0.2698
Complete DF = 9998
DF adjustment: Small sample DF: min = 131.79
avg = 148.15
max = 164.50
Model F test: Equal FMI F( 1, 131.8) = 53733.02
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9976108 .0043037 231.80 0.000 .9890976 1.006124
_cons | .0105094 .0156034 0.67 0.502 -.0202993 .0413181
------------------------------------------------------------------------------
On the other hand, x is distributed normally within each g group. If you impute the two groups separately then ordinary regression fits the data quite well:
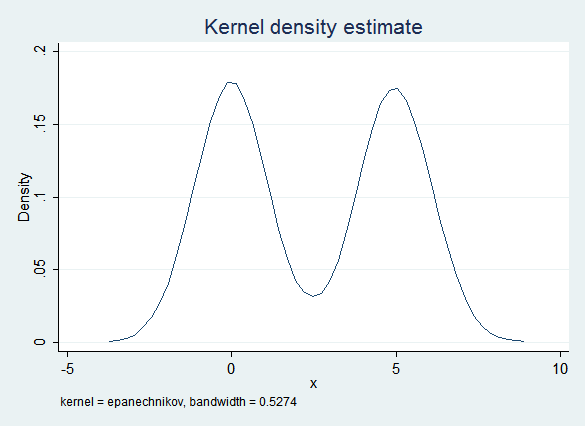
The regression results are also good:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.6503
Largest FMI = 0.4656
Complete DF = 9998
DF adjustment: Small sample DF: min = 45.53
avg = 63.49
max = 81.45
Model F test: Equal FMI F( 1, 81.4) = 48664.75
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9996345 .0045314 220.60 0.000 .9906191 1.00865
_cons | .0032657 .0183149 0.18 0.859 -.0336105 .0401419
------------------------------------------------------------------------------
Lessons Learned
PMM can be a very effective tool for imputing non-normal data. On the other hand, if you can identify groups whose data may vary in systematically different ways, consider imputing them separately.
However, the regression results were uniformly good, even when the data were imputed using the original regression model where the distribution of the imputed values didn't match the distribution of the observed values very well. In part this is because we had a large number of observations and a simple model, but in general the relationship between face validity and getting valid estimates using the imputed data is unclear.
Transformations
Given non-normal data, it's appealing to try to transform it in a way that makes it more normal. But what if the other variables in the model are related to the original values of the variable rather than the transformed values?
Complete code for this example
Data
Observations: 10,000
Variables:
- x1 is drawn from the standard normal distribution, then exponentiated. Thus it is log-normal
- x2 is drawn from the standard normal distribution
- y is the sum of x1, x2 and a normal error term
Missingness: x1, x2 and y have a 10% probability of being missing (MCAR)
Right Answers: Regressing y on x1 and x2, both should have a coefficient of 1.
Procedure
First, complete cases analysis for comparison. It does quite well, as we'd expect with MCAR data (and a simple model with lots of observations):
Source | SS df MS Number of obs = 7299
-------------+------------------------------ F( 2, 7296) =19024.33
Model | 38421.4045 2 19210.7023 Prob > F = 0.0000
Residual | 7367.47472 7296 1.00979643 R-squared = 0.8391
-------------+------------------------------ Adj R-squared = 0.8391
Total | 45788.8793 7298 6.27416816 Root MSE = 1.0049
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | 1.001594 .0057231 175.01 0.000 .9903751 1.012813
x2 | .9973623 .0117407 84.95 0.000 .9743471 1.020377
_cons | .0035444 .0149663 0.24 0.813 -.025794 .0328827
------------------------------------------------------------------------------
This data set presents a dilemma for imputation: x1 can be made normal simply by taking its log, but y is related to x1, not the log of x1. Regressing ln(x1) on x2 and y (as the obvious imputation model will do) results in the following plot of residuals vs. fitted values (rvfplot):
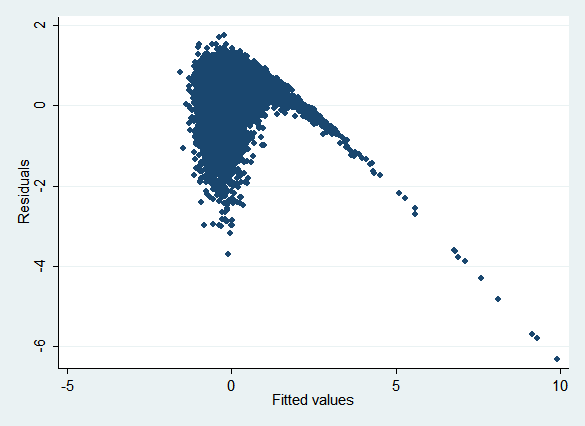
If the model were specified correctly, we'd expect the points to be randomly distributed around the y axis regardless of their x location. Clearly that's not the case.
The obvious way to impute this data would be to:
- Log transform x1 by creating lnx1 = ln(x1)
- Impute lnx1 using regression
- Create the passive variable ix1 = exp(lnx1) to reverse the transformation
Here are the regression results after doing so:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 196.4421
Largest FMI = 0.9987
Complete DF = 9997
DF adjustment: Small sample DF: min = 5.89
avg = 242.41
max = 701.09
Model F test: Equal FMI F( 2, 12.8) = 3.84
Within VCE type: OLS Prob > F = 0.0493
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ix1 | .014417 .0213705 0.67 0.525 -.0381112 .0669452
x2 | .9951566 .0235333 42.29 0.000 .9489525 1.041361
_cons | 1.583044 .0384844 41.13 0.000 1.502835 1.663253
------------------------------------------------------------------------------
As you see, the coefficient on ix1 (imputed untransformed x1) is very strongly biased towards zero. Now try imputing lnx1 using Predictive Mean Matching rather than regression:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.7058
Largest FMI = 0.6292
Complete DF = 9997
DF adjustment: Small sample DF: min = 24.80
avg = 53.56
max = 74.84
Model F test: Equal FMI F( 2, 52.8) = 8286.63
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ix1 | .9554301 .009311 102.61 0.000 .9362457 .9746144
x2 | .9537128 .0146582 65.06 0.000 .9245112 .9829144
_cons | .0843407 .0192948 4.37 0.000 .0457588 .1229226
------------------------------------------------------------------------------
Now both coefficients are biased towards zero, though not nearly as strongly.
What if we simply ignore the fact that x1 is not normally distributed and impute it directly? The results are actually better:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.3873
Largest FMI = 0.3401
Complete DF = 9997
DF adjustment: Small sample DF: min = 84.25
avg = 179.94
max = 337.16
Model F test: Equal FMI F( 2, 133.4) = 17538.58
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | .9980159 .0060605 164.68 0.000 .9859646 1.010067
x2 | .9912113 .0117879 84.09 0.000 .967869 1.014554
_cons | .0108679 .0140238 0.77 0.439 -.0167172 .038453
------------------------------------------------------------------------------
This clearly works well, but raises the question of face validity. Here is a kernel density plot of the observed values of x1:
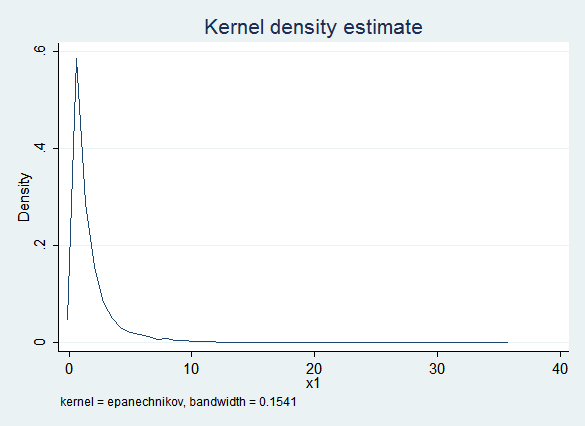
Here is a kernel density plot of the imputed values of x1:
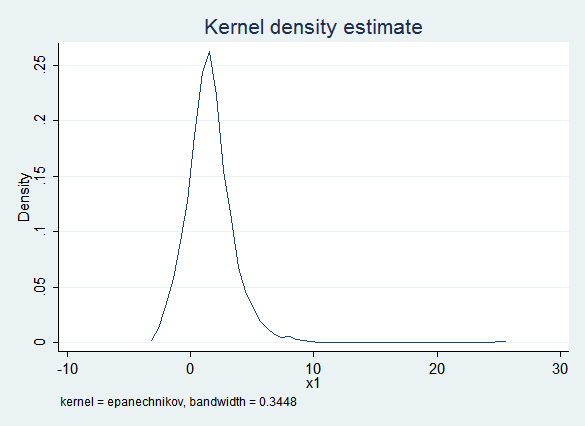
The obvious problem is that the imputed values of x1 are frequently less than zero while the observed values of x1 are always positive. This would be especially problematic if you thought you might want to use a log transform later in the process.
Given the constraint that x1 cannot be less than zero, truncreg seems like a plausible alternative. Unfortunately, truncreg fails to converge for this data set (for reasons not yet clear to us). But PMM will also honor that constraint:
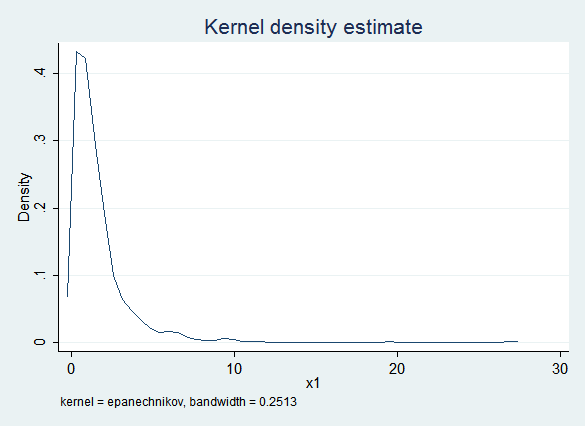
Here are the regression results with PMM:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.3702
Largest FMI = 0.3664
Complete DF = 9997
DF adjustment: Small sample DF: min = 72.89
avg = 147.11
max = 193.33
Model F test: Equal FMI F( 2, 145.1) = 17890.15
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | 1.000568 .0056325 177.64 0.000 .9894588 1.011677
x2 | .9977033 .012447 80.16 0.000 .9728958 1.022511
_cons | .009171 .014612 0.63 0.531 -.0196674 .0380094
------------------------------------------------------------------------------
Lessons Learned
The lesson of this example is not that you should never transform covariates. Keep in mind that what makes transforming x1 problematic in this example is that the relationship between y and x1 is known to be linear.
The real lesson is that misspecification in your imputation model can cause problems in your analysis model. Be sure to run the regressions implied by your imputation models separately and check them for misspecification. A secondary lesson is that PMM can work well for non-normal data.
Non-Linearity
Non-linear terms in your analysis model present a major challenge in creating an imputation model, because the non-linear relationship between variables can't be easily inverted.
Note: in this example we'll frequently use Stata's syntax for interactions to create squared terms. A varlist of c.x##c.x is equivalent to the varlist x x2 where x2 is defined by gen x2=x^2. The squared term shows up in the output as c.x#c.x. Using c.x##c.x is convenient because you don't have to create a separate variable, and because in that form post-estimation commands can take into account the fact that x and x^2 are not independent variables.
Complete code for this example
Data
Observations: 1,000
Variables:
- x is drawn from the standard normal distribution
- y is x plus x^2 plus a normal error term
Missingness: y and x have a 10% probability of being missing (MCAR).
Right Answers: Regressing y on x and x^2, both should have a coefficient of 1.
Procedure
First, complete cases analysis for comparison:
Source | SS df MS Number of obs = 815
-------------+------------------------------ F( 2, 812) = 1184.66
Model | 2350.4449 2 1175.22245 Prob > F = 0.0000
Residual | 805.533089 812 .992035824 R-squared = 0.7448
-------------+------------------------------ Adj R-squared = 0.7441
Total | 3155.97799 814 3.87712284 Root MSE = .99601
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9798841 .0344861 28.41 0.000 .9121917 1.047577
|
c.x#c.x | .9948393 .0244134 40.75 0.000 .9469185 1.04276
|
_cons | -.0047983 .0429475 -0.11 0.911 -.0890994 .0795029
------------------------------------------------------------------------------
The obvious thing to do is to impute x, then allow x^2 to be a passive function of x (it makes no difference whether you create a variable for x^2 using mi passive or allow Stata to do it for you by putting c.x##c.x in your regression). However, this means that the imputation model for x simply regresses x on y. This is misspecified, as you can see from an rvfplot:
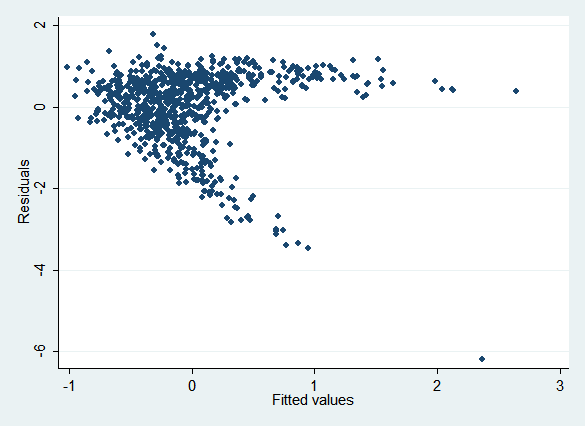
Here are the regression results. Because the imputation model is misspecified , the coefficient on x^2 (c.x#c.x) is biased:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.9729
Largest FMI = 0.5328
Complete DF = 997
DF adjustment: Small sample DF: min = 32.79
avg = 37.89
max = 46.68
Model F test: Equal FMI F( 2, 50.2) = 351.77
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9586506 .0570451 16.81 0.000 .8427484 1.074553
|
c.x#c.x | .844537 .0409527 20.62 0.000 .7611974 .9278765
|
_cons | .1986436 .0662195 3.00 0.004 .0654027 .3318845
------------------------------------------------------------------------------
Next impute x using PMM. It's an improvement but still biased:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.3974
Largest FMI = 0.3984
Complete DF = 997
DF adjustment: Small sample DF: min = 56.92
avg = 101.37
max = 134.94
Model F test: Equal FMI F( 2, 167.9) = 763.23
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9511347 .041403 22.97 0.000 .8691019 1.033167
|
c.x#c.x | .9170003 .027871 32.90 0.000 .8618798 .9721207
|
_cons | .1160666 .0565846 2.05 0.045 .0027546 .2293787
------------------------------------------------------------------------------
The include() option of mi impute chained is usually used to add variables to the imputation model of an individual variable, but it can also accept expressions. Does adding x^2 to the imputation for y with (regress, include((x^2))) y fix the problem? Unfortunately not, though it helps:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 1.1210
Largest FMI = 0.7256
Complete DF = 997
DF adjustment: Small sample DF: min = 17.48
avg = 70.29
max = 118.18
Model F test: Equal FMI F( 2, 39.1) = 377.13
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9629371 .0452655 21.27 0.000 .8727678 1.053106
|
c.x#c.x | .8874316 .0475562 18.66 0.000 .7873051 .9875581
|
_cons | .125851 .053619 2.35 0.021 .0196724 .2320296
------------------------------------------------------------------------------
The imputation model for y has been fixed, but the imputation model for x is still misspecified and this still biases the results of the analysis model. Unfortunately, the true dependence of x on y does not match any standard regression model.
Next we'll use what White, Royston and Wood (Multiple imputation using chained equations: Issues and guidance for practice, Statistics in Medicine, November 2010) call the "Just Another Variable" approach. This creates a variable to contain x^2 (x2) and then imputes both x and x2 as if x2 were "just another variable" rather than being determined by x. The obvious disadvantage is that in the imputed data x2 is not equal to x^2, so it lacks face validity. But the regression results are a huge improvement:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.2375
Largest FMI = 0.3033
Complete DF = 997
DF adjustment: Small sample DF: min = 92.98
avg = 331.43
max = 610.11
Model F test: Equal FMI F( 2, 496.2) = 1330.20
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9905117 .0324469 30.53 0.000 .9267905 1.054233
x2 | 1.005361 .0240329 41.83 0.000 .9580613 1.052662
_cons | -.0018354 .046395 -0.04 0.969 -.0939669 .0902961
------------------------------------------------------------------------------
So would imputing x and x2 using PMM be even better on the theory that PMM is better in sticky situations of all sorts? Not this time:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 1000
Average RVI = 0.3068
Largest FMI = 0.3151
Complete DF = 997
DF adjustment: Small sample DF: min = 86.95
avg = 201.95
max = 312.22
Model F test: Equal FMI F( 2, 163.9) = 1138.59
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9761798 .0346402 28.18 0.000 .9078863 1.044473
x2 | .9987715 .0258422 38.65 0.000 .947407 1.050136
_cons | -.0032279 .0416431 -0.08 0.938 -.0851645 .0787087
------------------------------------------------------------------------------
Lessons Learned
Again, the principal lesson is that misspecification in your imputation model can lead to bias in your analysis model. Be very careful, and always check the fit of your imputation models.
This is a continuing research area, but there appears to be some agreement that imputing non-linear terms as passive variables should be avoided. "Just Another Variable" seems to be a good alternative.
Interactions
Interaction terms in your analysis model also lead to challenges in creating an imputation model because it should take into account the interaction in the model for the covariates being interacted.
Note: we'll again use Stata's syntax for interactions. Putting g##c.x in the covariate list of a regression regresses the dependent variable on g, continuous variable x, and the interaction between g and x. The interaction term shows up in the output as g#c.x.
Complete code for this example
Data
Observations: 10,000
Variables:
- g is a binary (1/0) variable with a 50% probability of being 1
- x is drawn from the standard normal distribution
- y is x plus x*g plus a normal error term. Put differently, y is x plus a normal error term for group 0 and 2*x plus a normal error term for group 1.
Missingness: y and x have a 20% probability of being missing (MCAR).
Right Answers: Regressing y on x, g, and the interaction between x and g, the coefficients for x and the interaction term should be 1, and the coefficient on g should be 0.
Procedure
The following are the results of complete cases analysis:
Source | SS df MS Number of obs = 6337
-------------+------------------------------ F( 3, 6333) = 5435.30
Model | 16167.6705 3 5389.2235 Prob > F = 0.0000
Residual | 6279.30945 6333 .991522099 R-squared = 0.7203
-------------+------------------------------ Adj R-squared = 0.7201
Total | 22446.98 6336 3.5427683 Root MSE = .99575
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.g | -.012915 .0250189 -0.52 0.606 -.0619605 .0361305
x | .9842869 .017752 55.45 0.000 .9494869 1.019087
|
g#c.x |
1 | 1.026204 .0249124 41.19 0.000 .9773671 1.075041
|
_cons | -.0195648 .0177789 -1.10 0.271 -.0544175 .0152879
------------------------------------------------------------------------------
The obvious way to impute this data is to impute x and create the interaction term passively. However that means x is regressed on y and g without any interactions. The result is biased estimates (in opposite directions) of the coefficients for both x and the interaction term:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.5760
Largest FMI = 0.3048
Complete DF = 9996
DF adjustment: Small sample DF: min = 104.17
avg = 130.43
max = 182.89
Model F test: Equal FMI F( 3, 205.4) = 4870.03
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.g | -.0077291 .0251103 -0.31 0.759 -.0575089 .0420506
x | 1.119861 .0182704 61.29 0.000 1.083631 1.156091
|
g#c.x |
1 | .7300249 .0239816 30.44 0.000 .6827087 .777341
|
_cons | -.0148091 .0174857 -0.85 0.399 -.0494078 .0197896
------------------------------------------------------------------------------
An alternative approach is to create a variable for the interaction term, gx, and impute it separately from x (White, Royston and Wood's "Just Another Variable" approach). As in the previous example with a squared term, the obvious disadvantage is that the imputed value of gx will not in fact be g*x for any given observation. However, the results of the analysis model are much better:
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.4359
Largest FMI = 0.3753
Complete DF = 9996
DF adjustment: Small sample DF: min = 69.58
avg = 111.30
max = 210.61
Model F test: Equal FMI F( 3, 223.1) = 5908.62
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .9832953 .0159157 61.78 0.000 .9519209 1.01467
xg | 1.018901 .0239421 42.56 0.000 .9713602 1.066443
g | -.0141319 .0247797 -0.57 0.570 -.0635346 .0352709
_cons | -.0087754 .0176281 -0.50 0.620 -.0439374 .0263866
------------------------------------------------------------------------------
Another alternative is to impute the two groups separately. This allows x to have the proper relationship with y in both groups. However, it also allows the relationships between other variables to vary between groups. If you know that some relationships do not vary between groups you'll lose some precision by not taking advantage of this knowledge, but in the real world it's rare know such things.
Multiple-imputation estimates Imputations = 10
Linear regression Number of obs = 10000
Average RVI = 0.3627
Largest FMI = 0.3482
Complete DF = 9996
DF adjustment: Small sample DF: min = 80.48
avg = 218.72
max = 369.37
Model F test: Equal FMI F( 3, 456.6) = 6783.26
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.g | -.0218404 .0243087 -0.90 0.372 -.0702117 .0265309
x | .9869436 .0156451 63.08 0.000 .9561207 1.017766
|
g#c.x |
1 | 1.018534 .0214947 47.39 0.000 .976267 1.060802
|
_cons | -.0076746 .0158825 -0.48 0.629 -.0390027 .0236534
------------------------------------------------------------------------------
Lessons Learned
Once again, the principal lesson is that misspecification in your imputation model can lead to bias in your analysis model. Be very careful, and always check the fit of your imputation models.
This is also an area of ongoing research, but there appears to be some agreement that imputing interaction effects passively is problematic. If your interactions are all a matter of variables having different effects for different groups, imputing each group separately is probably the obvious solution, though "Just Another Variable" also works well. If you have interactions between continuous variables then use "Just Another Variable."
Acknowledgements
Some of these examples follow the discussion in White, Royston, and Wood. ("Multiple imputation using chained equations: Issues and guidance for practice." Statistics in Medicine. 2011.) We highly recommend this article to anyone who is learning to use multiple imputation.
Next: Recommended Readings
Previous: Estimating
Last Revised: 6/21/2012